lfsr可化为矩阵运算的性质

由于lfsr的线性的生成方法
我们可以将lfsr的实现过程用矩阵表示

[ByteCTF2025 magic_lfsr]
爆破一下这个ff就行了吧
真值表大法dddd

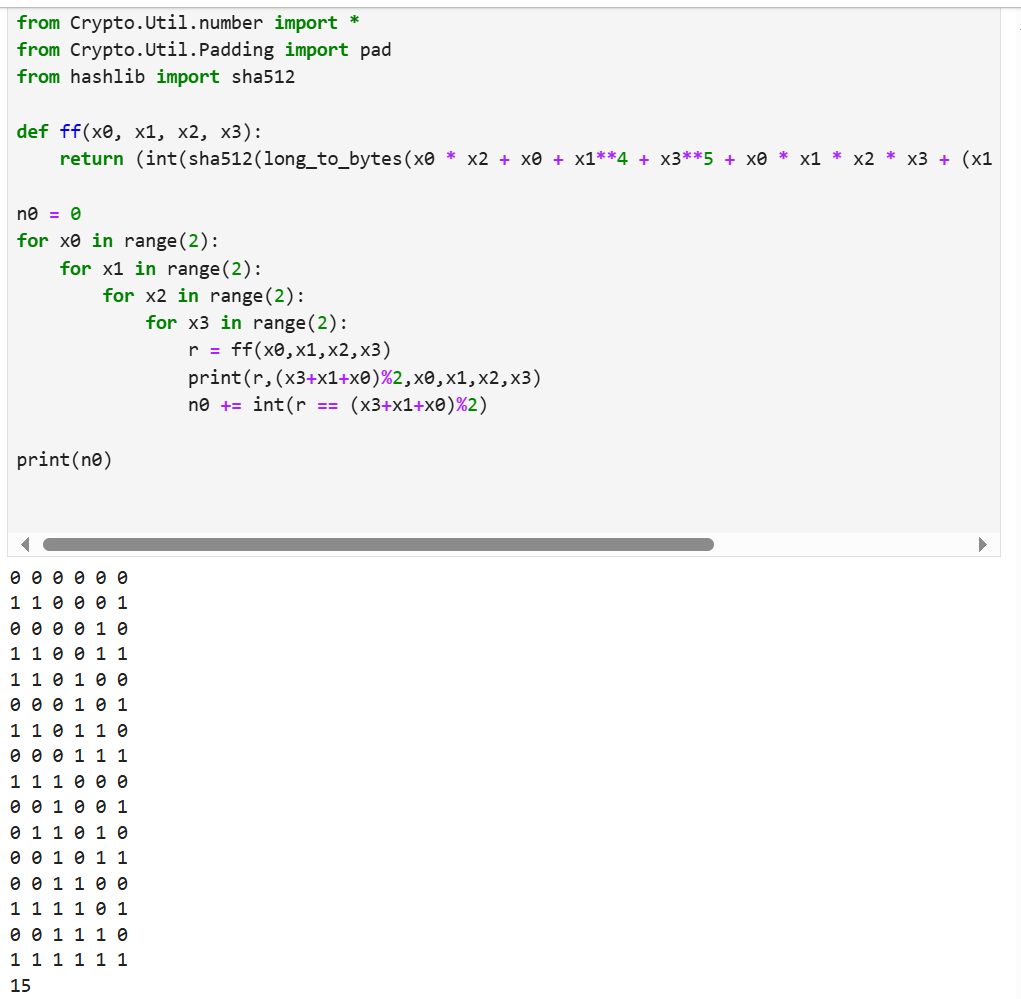
发现唯一的差异在0时出现，因此选取所有的1值（总共127个）造矩阵，剩下一个把所有的0值选取一遍总有一个是对的

from Crypto.Cipher import AES
from Crypto.Util.number import *
from Crypto.Util.Padding import pad
from hashlib import sha512
from copy import deepcopy

out = 1024311481407054984168503188572082106228007820628496173132204098971130766468510095
enc = b'\r\x9du\xa15q\xd2\x81\x0b\xceq2\x8d)*\xe9\xf0;a\xad\xbe?\xa2\xb2\x1f\x88O\x8c\xa2[\xcb\x9a\xa9\x8d\xac\x0b\x85\xb4j@]\x0e}EF{\xb1\x91'


mask1 = 211151158277430590850506190902325379931
mask2 = 314024231732616562506949148198103849397
mask3 = 175840838278158851471916948124781906887
mask4 = 270726596087586267913580004170375666103

m = matrix(GF(2),128,129)
M1,M2,M3 = matrix(GF(2),128,128),matrix(GF(2),128,128),matrix(GF(2),128,128)

for i in range(128):
    M1[i,0] = int(bin(mask1)[2:][i])
    M2[i,0] = int(bin(mask2)[2:][i])
    M3[i,0] = int(bin(mask4)[2:][i])
    if i != 127:
        M1[i,i+1] = 1
        M2[i,i+1] = 1
        M3[i,i+1] = 1

out = bin(out)[2:].zfill(270)
print(out)
si = []
for i in range(270):
    if out[i] == '1':
        si.append(i)
print(si,len(si))

n = 0
MM1,MM2,MM3 = identity_matrix(GF(2),128),identity_matrix(GF(2),128),identity_matrix(GF(2),128)
MM1 *= M1
MM2 *= M2
MM3 *= M3
for i in range(270):
    MM1 *= M1
    MM2 *= M2
    MM3 *= M3
    if i in si:
        m[:,n] = (MM1+MM2+MM3)[:,0]
        n += 1

assert n == 127
output = matrix([1]*127+[0]*2)
MM1,MM2,MM3 = identity_matrix(GF(2),128),identity_matrix(GF(2),128),identity_matrix(GF(2),128)
MM1 *= M1
MM2 *= M2
MM3 *= M3
for i in range(270):
    MM1 *= M1
    MM2 *= M2
    MM3 *= M3
    if i not in si:
        m[:,-2] = (MM1+MM2+MM3)[:,0]
        MMM1,MMM2,MMM3 = deepcopy(MM1),deepcopy(MM2),deepcopy(MM3)
        for j in range(i+1,270):
            MMM1 *= M1
            MMM2 *= M2
            MMM3 *= M3
            if j not in si:
                m[:,-1] = (MMM1+MMM2+MMM3)[:,0]
                try:
                    key = (m.solve_left(output))[0]
                    key = ''.join(str(_) for _ in key)
                    key = int(key,2)
                    cipher = AES.new(long_to_bytes(key), mode=AES.MODE_ECB)
                    print(cipher.decrypt(enc))
                except:
                    continue

可以看出来用矩阵运算的方法，求key时确定结果为127个1和剩下的一个0，mask就是我们用矩阵表示的M1+M2+M3的连乘
总的来看 mask作为右边的乘子一般可以表示为

上述为一个例子

就出题来看 在特定范围的爆破
从来都是原始又巧妙的设计思路

当爆破的范围隐藏的越隐蔽时 效果越好